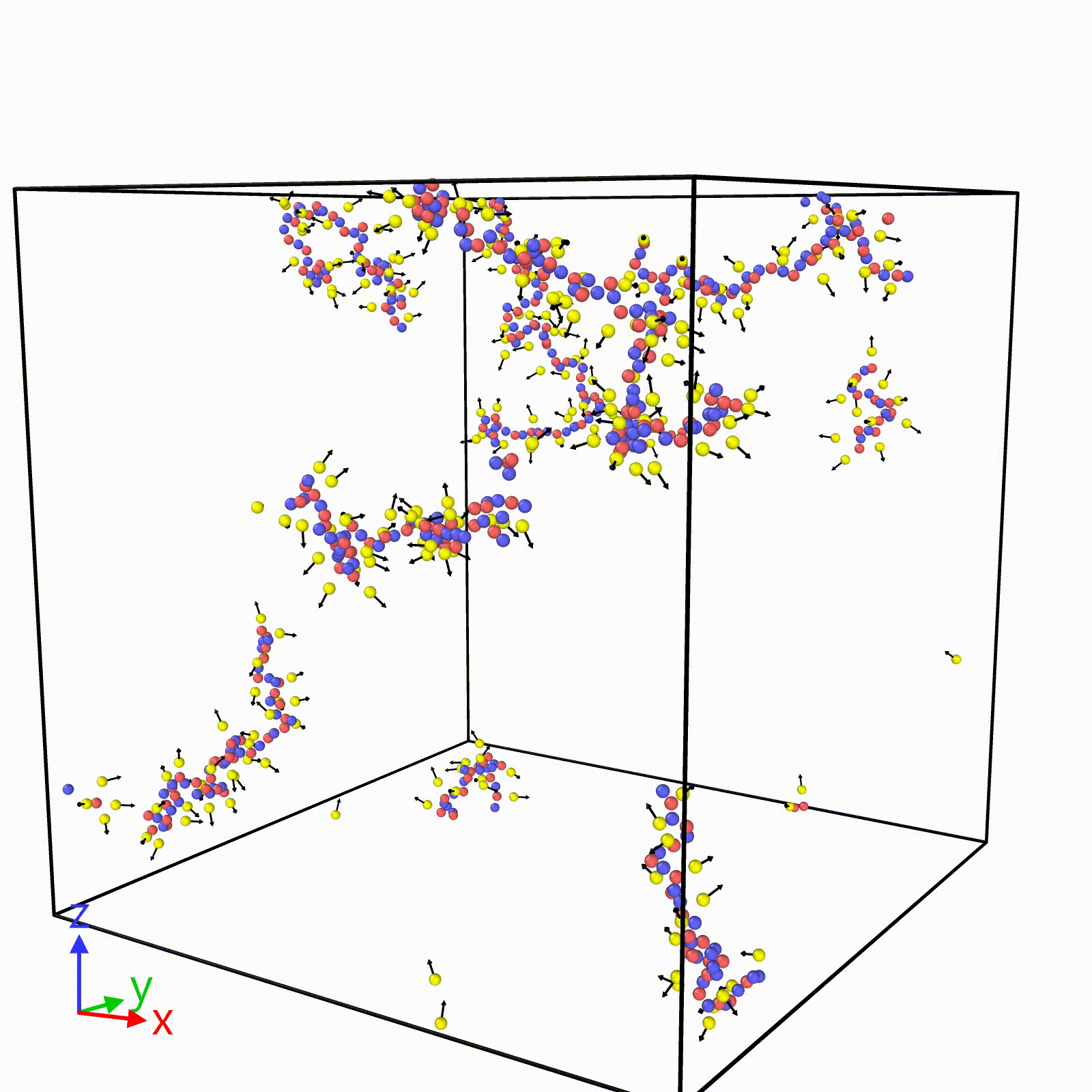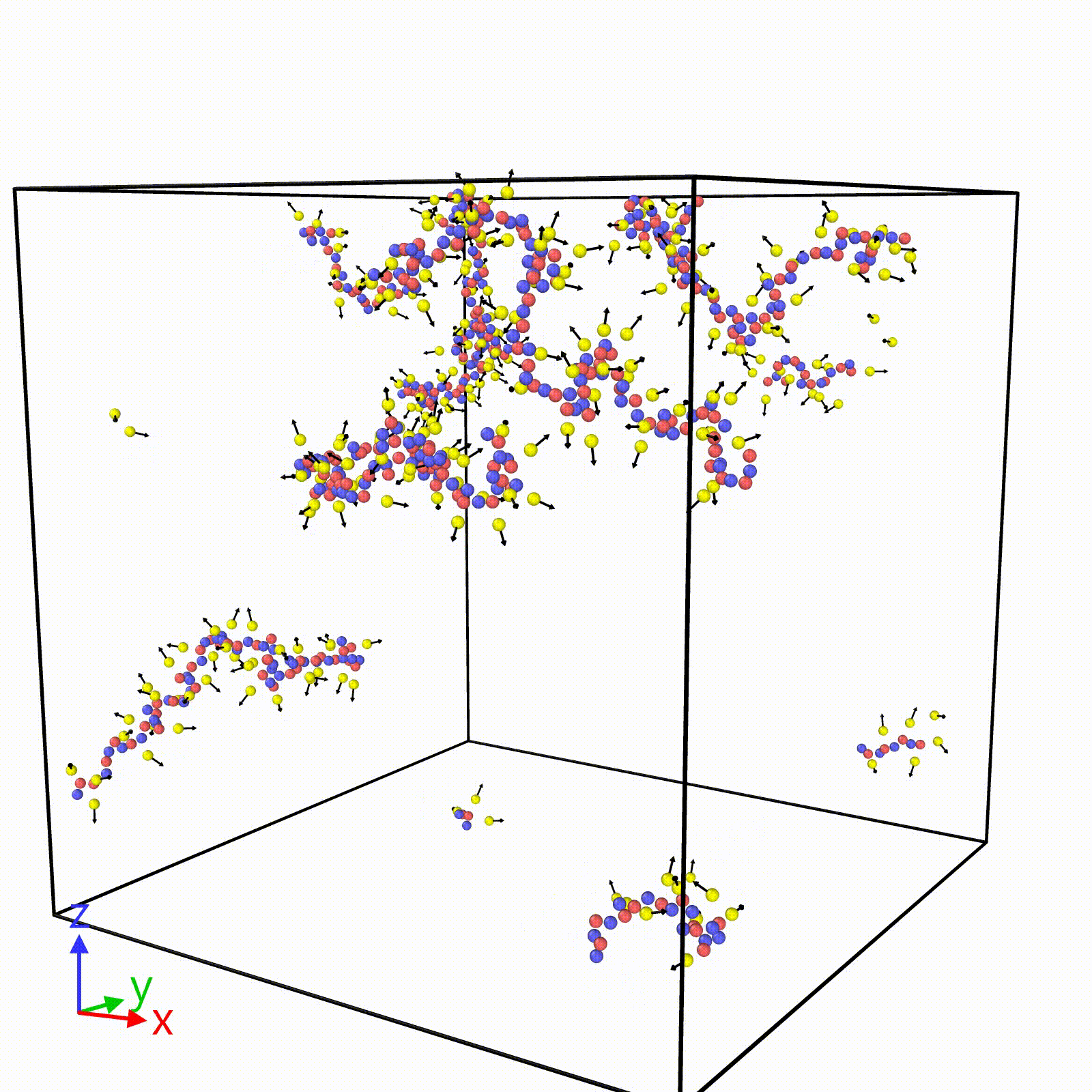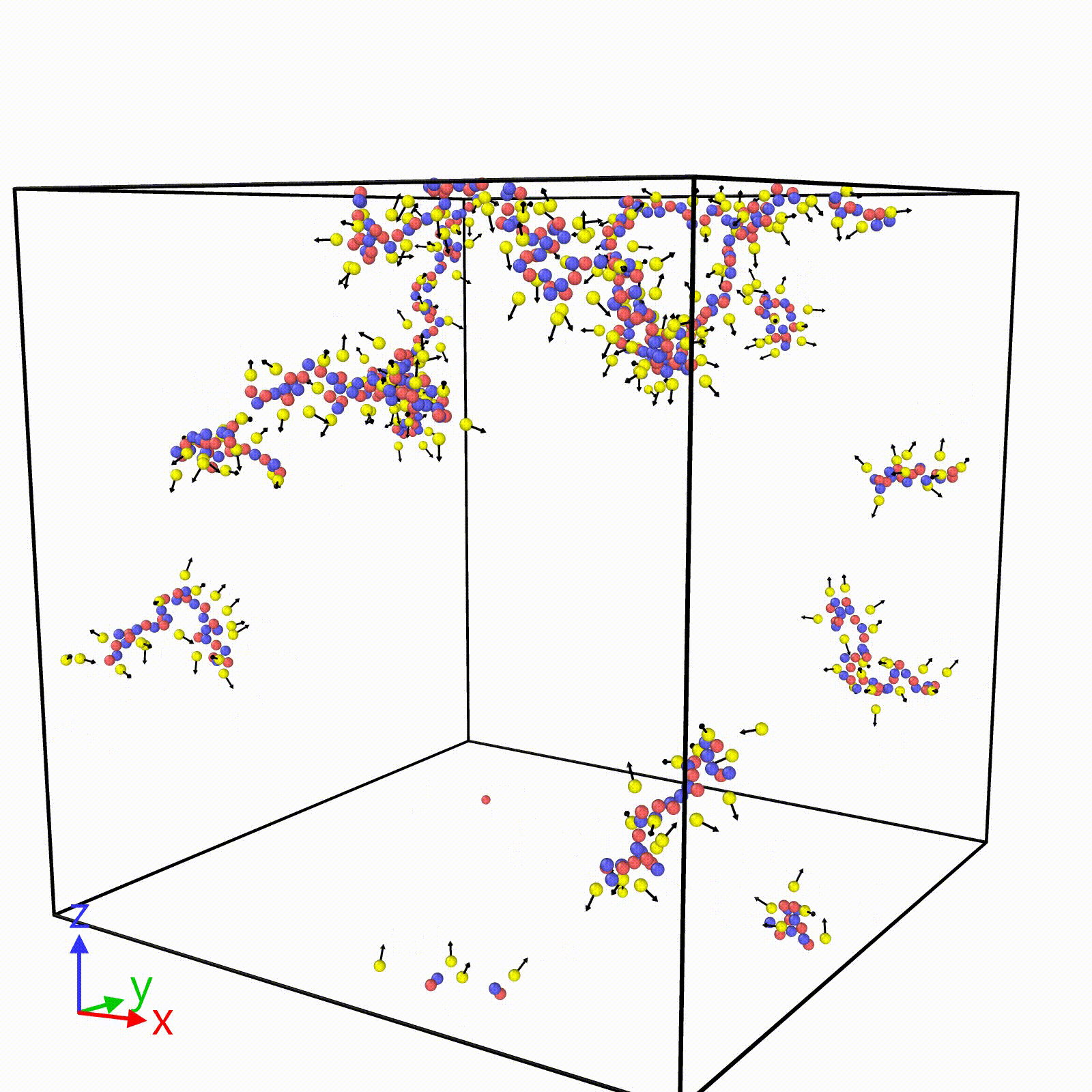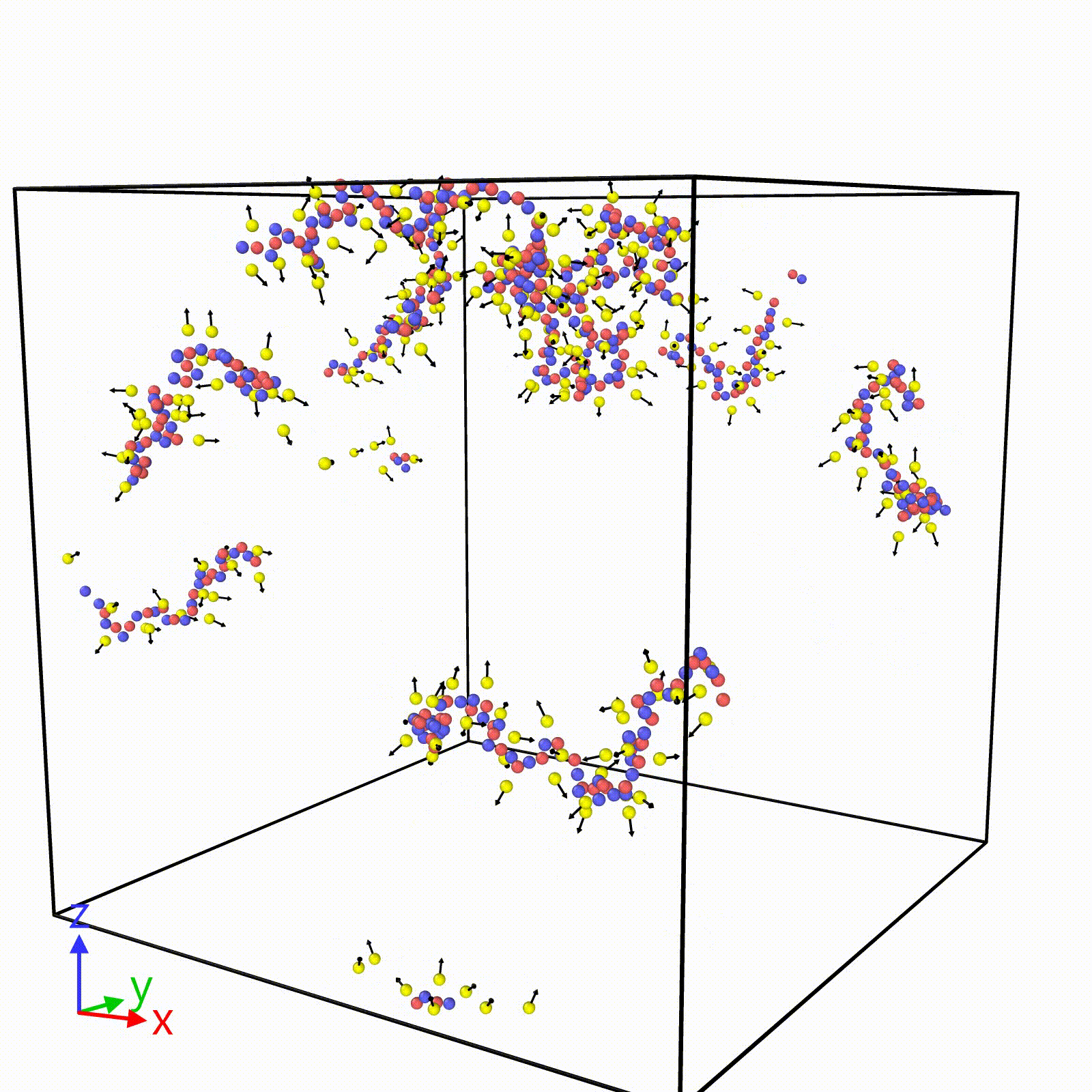
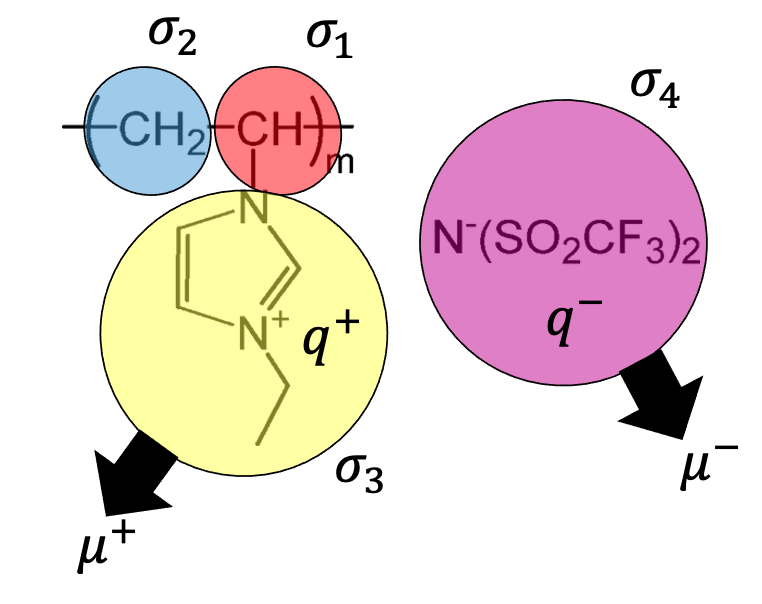
Molecular Dynamics Simulations for Non-Polymeric and Polymeric Ionic Liquids: Our research group specializes in developing coarse-grained molecular dynamics (MD) simulations based on Stockmayer fluids, with a particular focus on polymeric ionic liquids. These simulations offer a significant advantage by allowing us to explore extended timescales, surpassing even 100 nanoseconds, which is crucial for studying polymer electrolytes. This capability enables us to efficiently collect extensive statistical samples, enhancing the robustness of our findings.

The simplicity of our coarse-grained models is key to identifying the molecular parameters that critically influence target properties such as dielectric constant, viscosity, glass transition temperature, and ionic conductivity. Despite the model’s simplicity, our simulations consistently align with these experimental results across various systems, including ion-containing common solvents, ionic liquids, and even the dielectric constant of salt-doped water. Our approach not only accelerates the research process but also provides valuable insights into the fundamental behavior of these complex systems.

 

 

 

 

 

 

 

References

  • Shock, J. C., Stevens, M., Frischknecht, A., and Nakamura, I., “Molecular dynamics simulations of the dielectric constants of salt-free and salt-doped polar solvents”, J. Chem. Phys. 159, 134507 (2023)
  • Gao, T., Shock, C. J., Stevens, M. J., Frischknecht, A. L., and Nakamura, I., “Surrogate Molecular Dynamics Simulation Model for Dielectric Constants with Ensemble Neural Networks”, MRS Communications 12, 966–974 (2022)
  • Shock, C., Stevens, M., Frischknecht, A., and Nakamura, I., “Solvation Energy of Ions in a Stockmayer Fluid”, J. Phys. Chem. B 2020, 124, 22, 4598–4604
  • Gao, T., Itliong J., Kumar S. P., Hjorth Z., and Nakamura, I, “Polarization of Ionic Liquid and Polymer and its Implications for Polymerized Ionic Liquids: An Overview Towards a New Theory and Simulation”, J Polym Sci., 59, 2434–2457 (2020)
  • Nakamura, I., “Microphase Separation of Ionic Liquid-containing Diblock Copolymers: Effects of Dielectric Inhomogeneity and Asymmetry in the Molecular Volumes and Interactions between the Cation and Anion”, Macromolecules 2020, 53, 10, 3891–3899
  • Liu, L and Nakamura, I., “Solvation Energy of Ions in Polymers: Effects of Chain Length and Connectivity on Saturated Dipoles Near Ions”, Phys. Chem. B, 121, 3142-3150 (2017)

 

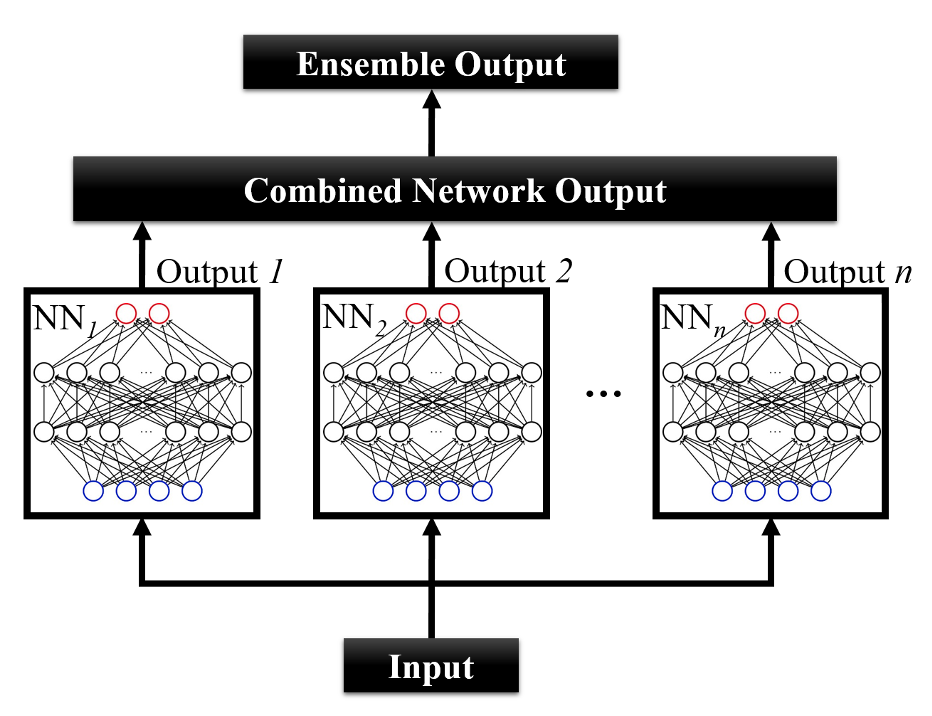
Machine Learning Application to Soft-Condensed Matter Physics: Our research group is dedicated to advancing the application of machine learning in the study of soft-condensed matter systems. Recognizing the challenges in determining model parameters that align with multiple experimental data sets, we are developing innovative strategies to overcome these computational hurdles. By constructing surrogate models using artificial neural networks, we aim to replicate the outcomes of our coarse-grained molecular dynamics simulations efficiently.

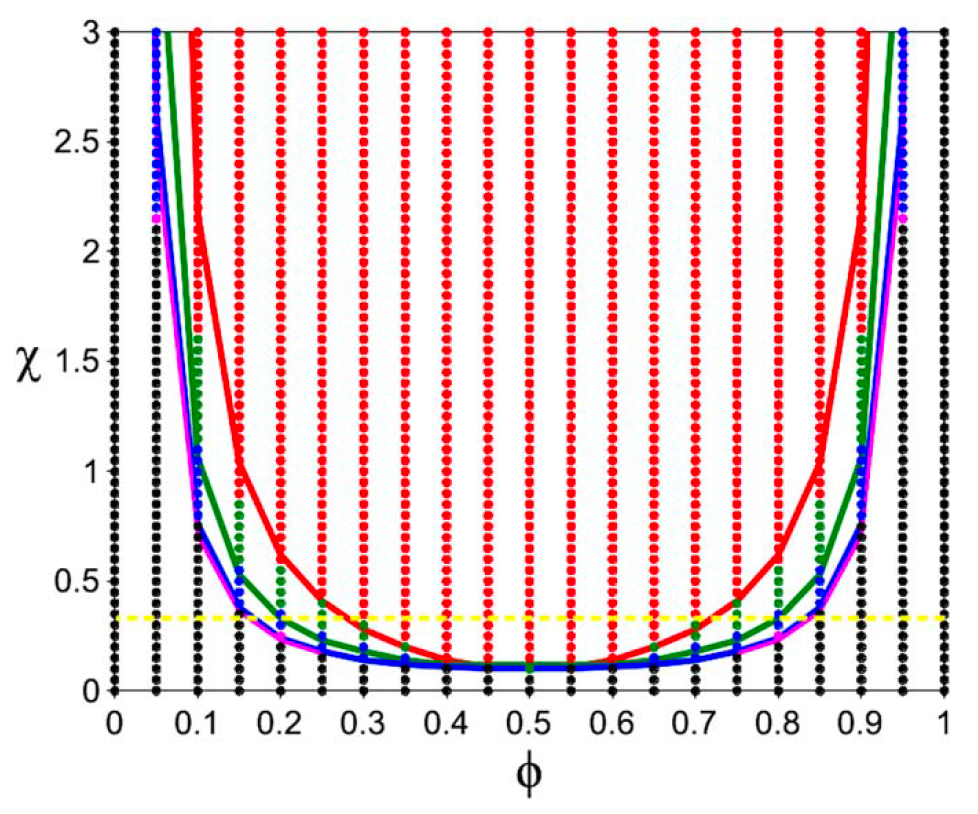
Our efforts include creating generative models that accurately predict experimental data, such as block copolymer microphase separations and microbial biodegradation in freshwater environments. Additionally, we are pioneering the use of neural networks to learn and apply complex statistical thermodynamics theories, like the random-phase approximation for phase diagrams in diblock copolymers. This approach bypasses traditional computational methods, offering both efficiency and the ability to generalize theoretical models to a broader range of systems.

 

LAM, GYR, HEX, BCC, and DIS phases predicted by our neural network, which aligns with Leibler’s mean-field theory.

 

 

 

 

 

 

 

 

 

References

  • Gao, T., Shock, C. J., Stevens, M. J., Frischknecht, A. L., and Nakamura, I., “Surrogate Molecular Dynamics Simulation Model for Dielectric Constants with Ensemble Neural Networks”, MRS Communications 12, 966–974 (2022)
  • Gao, T., Qian Z., Chen H., Shahbazian-Yassar R., and Nakamura, I, “Inhibition of Lithium Dendrite Growth with Highly Concentrated Ions: Cellular Automaton Simulation and Surrogate Model with Ensemble Neural Networks”, Mol. Syst. Des. Eng., 7, 260-272 (2022)
  • Nakamura, I, “Phase diagrams of polymer-containing liquid mixtures with a theory-embedded neural network”, New J. Phys. 22 (2020) 015001