When studying quantum mechanics in college, during the first month, you typically encounter the Schrödinger equation and the Hamiltonian, which govern the dynamics of a quantum system (for example, an electron in a square potential well). You learn that quantum operators, such as the Hamiltonian or momentum, are required to satisfy the Hermitian condition so that their eigenvalues are real numbers, which correspond to physically observable quantities.

In 1998, Bender and Boettcher discovered that a broad class of Hamiltonians, even if non-Hermitian, can still have entirely real eigenvalues, provided they obey parity-time (PT) symmetry. This surprising concept was first realized in optics and later extended to other physical systems, including acoustics, atomic systems, mechanics, and electronics.

Over the past two decades, PT symmetry and non-Hermitian physics have permeated many areas of physics and are now widely recognized. My research focuses on PT symmetry and non-Hermiticity in optics, both in fundamental studies and in practical applications. In particular, my main research direction is the study of singular points—so-called exceptional points—in PT-symmetric and non-Hermitian systems.

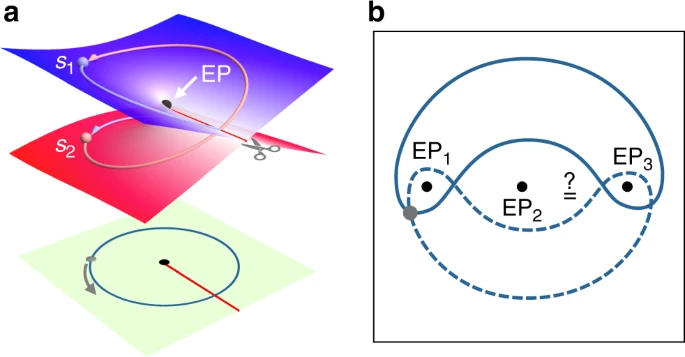
Related publications:

(1) Nature Communications 9, 4808 (2018)
(2) Physical Review Letters 122, 153902 (2019)
(3) Physical Review Letters 125, 203602 (2020)

Micro/nanophotonics

Light can be manipulated by lenses, prisms, and other bulk optical instruments, enabling technologies such as cameras, telescopes, and VR headsets. These applications rely on guiding light to form images in our eyes. Beyond imaging, light also serves as an excellent carrier of information—much like electricity. Optical fibers are a prime example, forming the backbone of the modern internet society.

Light is an electromagnetic wave, with visible wavelengths ranging roughly from 400 to 700 nm. At this scale, controlling and manipulating the propagation of light is the focus of micro/nanophotonics. By engineering light–matter interactions on these scales, we can unlock applications in optical computing and even quantum optical computation.

My research explores new physical concepts to design advanced photonic structures, such as optical lattices, waveguide couplers, and optical microcavities. We combine emerging tools—artificial intelligence (AI), inverse design techniques, and numerical electromagnetic simulations (e.g., COMSOL, Lumerical FDTD)—to create novel micro/nano-optical devices and to investigate fascinating phenomena of light at these scales.

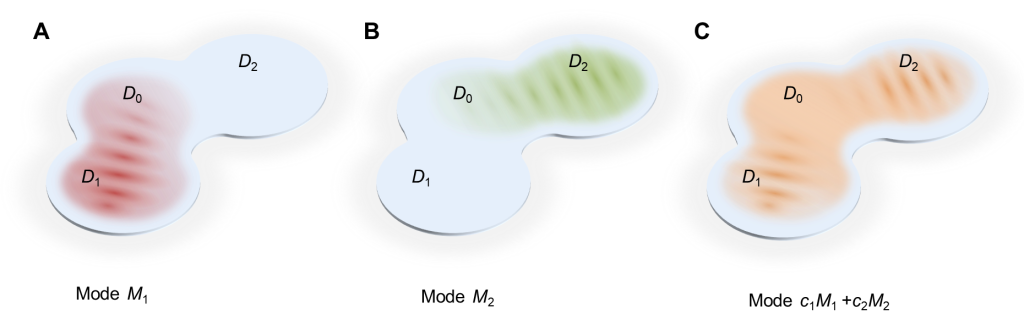
Related publications:

(1) Photonics Research 7, 1240 (2019)
(2) Nanophotonics 11, 4427 (2022)
(3) Light: Science & Applications 13, 65 (2024)

Optical thermodynamics

“Ludwig Boltzmann, who spent much of his life studying statistical mechanics, died in 1906, by his own hand. Paul Ehrenfest, carrying on the work, died similarly in 1933. Now it is our turn to study statistical mechanics.” —David L. Goodstein, “States of Matter”.

Thermodynamics describes how heat, work, temperature, and energy behave in matter. Statistical mechanics provides the microscopic foundation for these concepts by explaining how the collective behavior of many particles gives rise to thermodynamic laws.

A famous example is the Fermi–Pasta–Ulam–Tsingou (FPUT) problem, where Fermi and collaborators used one of the earliest computers to simulate vibrations in a one-dimensional chain. They asked whether introducing nonlinearity would cause energy to spread across all vibration modes and eventually lead to chaos and thermal equilibrium.

Today, similar questions can be posed in optical systems. In multimode fibers, coupled optical waveguide arrays, or optical cavities with a large but finite number of modes, nonlinear interactions can drive thermodynamic-like processes. In the linear regime, energy launched into a set of modes remains fixed in those modes. However, even weak nonlinearities introduce interactions between modes, allowing energy to flow and redistribute.

If the system becomes sufficiently chaotic, it may relax to a stationary state. In this state, conservation laws—such as energy conservation—constrain the distribution of energy among modes. For example, light in such systems can follow the Rayleigh–Jeans distribution, analogous to how collisions between molecules in a gas redistribute energy and ultimately produce the Maxwell–Boltzmann distribution.

Our research aims to understand the mechanisms of thermalization in nonlinear optical systems and to explore the novel optical phenomena that emerge from this framework.

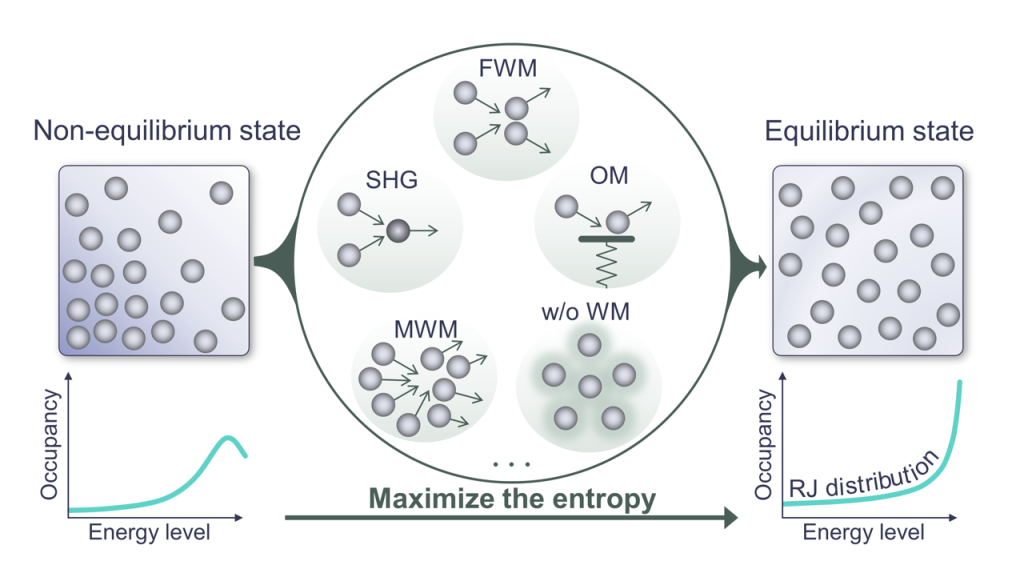
Related publications

(1) Physical Review Letters 128, 123901 (2022)
(2) Nature Communications 14, 370 (2023)
(3) Light: Science & Applications 14 (1), 188 (2025)

From Single Photon to Entanglement

The nature of light has fascinated scientists for centuries. Newton believed light was made of particles, while Huygens and others proposed that it was a wave. This wave nature was later confirmed by experiments such as Young’s double-slit interference and the Poisson spot. In the 19th century, Maxwell unified electricity and magnetism and showed that light is an electromagnetic wave, a prediction verified experimentally by Hertz.

In 1905, Einstein introduced the concept of light quanta to explain the photoelectric effect, laying the foundation of quantum optics. Decades later, experimental techniques allowed physicists to generate and manipulate individual photons in the laboratory. Richard Feynman famously remarked that single-photon interference in the double-slit experiment embodies the “heart of quantum mechanics.” In 1935, Einstein, Podolsky, and Rosen raised fundamental questions about quantum mechanics in their famous paper, introducing the concept of entanglement. Entangled photon pairs were eventually realized and confirmed experimentally, opening new frontiers in both fundamental physics and quantum technologies.

Our lab continues this pursuit of light on both microscopic and fundamental levels. We generate single photons, photon pairs, and entangled states, and study their quantum interference and correlations. We design single-photon interferometers, investigate new quantum effects with two-photon and entangled states, and explore how micro/nanophotonic structures can be harnessed to manipulate quantum light.

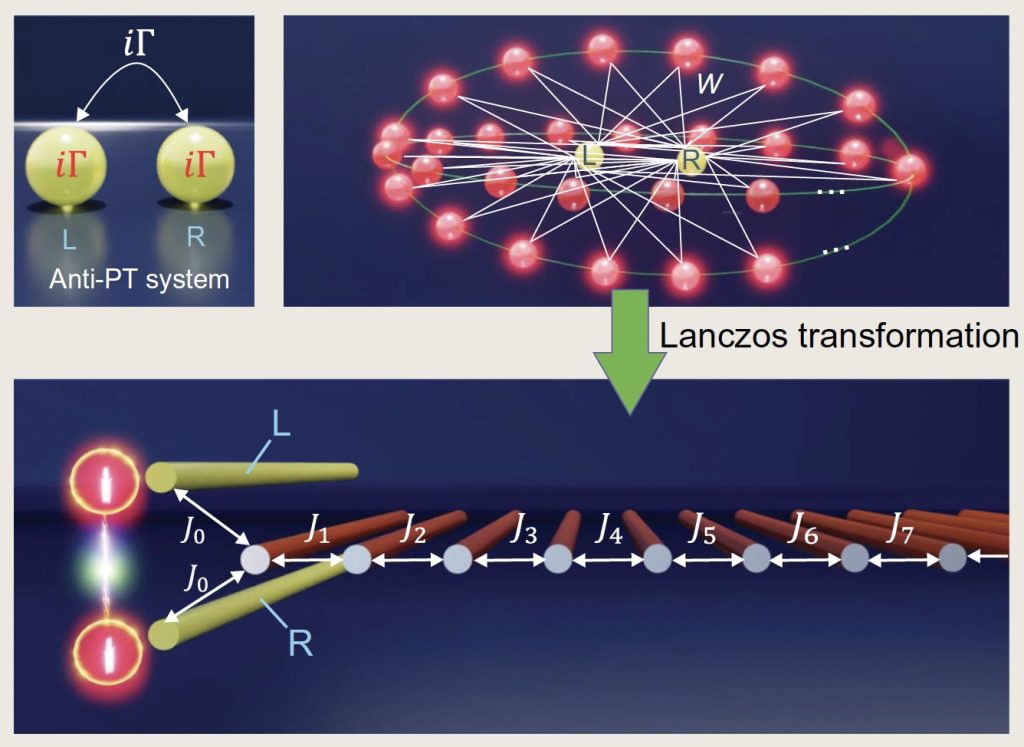
Related publications

(1) CLEO: QELS_Fundamental Science, FTh2J. 6 (2021)
(2) Physical Review Research 3, 013220 (2021)
(3) Science 387 (6741), 1424 (2025)